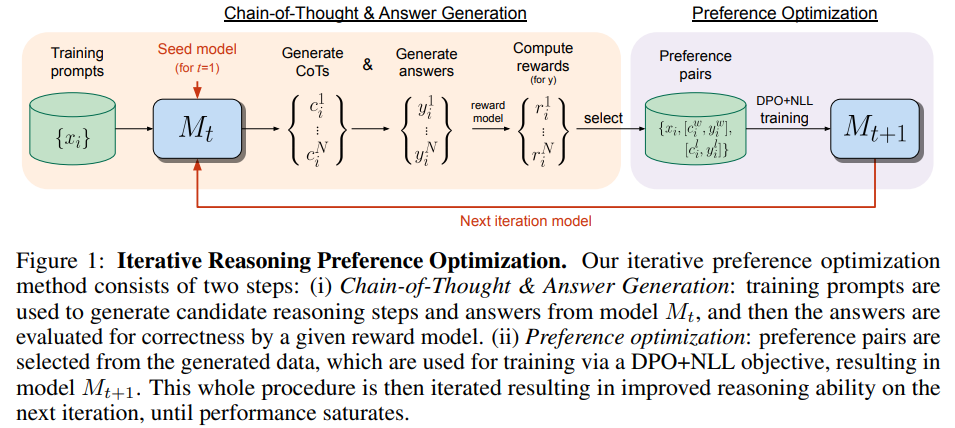
Iterative Reasoning Preference Optimization

논문 링크

• 논문 링크
• 발표 기관: Meta, New York University

Overview

• DPO가 일반적인 task에서는 좋은 성능을 보이지만, reasoning task에서는 성능 향상이 높지 못하다.
• 이것을 개선하기 위해서, 아래 두 가지 방법을 제안한다.
  • Chain-of-Thought를 포함한 결과물에 대해서 DPO를 iterative 하게 수행한다.
  • 모델을 학습할 때, DPO loss 뿐만 아니라 NLL (negative log likelihood) loss도 같이 학습시킨다.
• 이렇게 하면, 각종 reasoning task (e.g. GSM8K, MATH 등)에서 큰 성능 향상을 보인다.

Iterative Reasoning Preference Optimization

• DPO로 학습한 모델을 이용해서 Chain-of-Thought + 정답을 N개 생성하게 한 뒤, 그걸 데이터셋으로 삼아서 다시 DPO를 학습시키는 방식.
• 따라서 language model이 기본적으로 reasoning step을 생성하고, 답을 생성하는 능력을 가지고 있어야 한다.
• 또한, LM이 생성한 답변에서 preference pair를 뽑아내야 하는데, 여기서는 실제 정답을 놓고, 맞춘 것과 틀린 것으로 pair를 구성했다.

학습 방법

• Loss function은 아래 두 개의 term으로 구성된다. w는 이긴 (정답을 맞춘) 데이터, l는 진 (정답을 틀린) 데이터셋이다. c는 chain-of-thought 데이터, y는 정답 데이터를 의미한다. 이 loss는 t+1번째 iteration에서의 loss이다.

\[L_{DPO+NLL} = L_{NLL}(x_i,c_i^w,y_i^w) + \alpha L_{DPO}(c_i^w,y_i^w,c_i^l,y_i^l|x_i)\]

• 각각의 Loss는 아래와 같다.

\[L_{NLL} = -\frac{\log{M_{\theta}(x_i,c_i^w,y_i^w)}}{|x_i|+|c_i^w|+|y_i^w|}\] \[L_{DPO} = \log{\sigma (\beta \frac{\log{M_{\theta}(c_i^w,y_i^w|x_i)}}{\log{M_t(c_i^w,y_i^w|x_i)}} - \beta \frac{\log{M_{\theta}(c_i^l,y_i^l|x_i)}}{\log{M_t(c_i^l,y_i^l|x_i)}})}\]

• 이 학습은 t번째 모델에서 생성된 데이터로 이루어지며, 학습 데이터 $D = {x_i, y_i}$를 이용해서 생성하고, reward까지 측정한 데이터셋이다.

\[G_i = \{c_i^n,y_i^n,r_i^n\}_{n \in [1,N] }\]

• 여기에서는 정답을 맞췄는지, 틀렸는지로 구분하기 때문에, winner 그룹과 loser 그룹이 각각 아래처럼 나눠진다.
  • 여기서 K개의 페어를 구성함으로써 데이터셋을 만든다.
  \[G_i^w = \{c_i^n,y_i^n|r_i^n=1\} \text{ and } G_i^l=\{c_i^n,y_i^n|r_i^n=0\}\]
• Iterative Training
  • 기존의 방식에 비해서 간단한데, Self-Rewarding LLM training 방식은 그 때마다 생성된 새로운 prompt를 사용하고, 그러다보니 복잡한 reward model이 필요하다. 우리 방식은 gold label을 사용하고, 고정된 prompt를 쓰기 때문에 간단하다.
  • Self-Taught Reasoning 방식과도 유사하지만, STaR은 SFT 학습을 하는데 반해서 우리는 preference optimization을 한다.

실험

• GSM8K의 결과
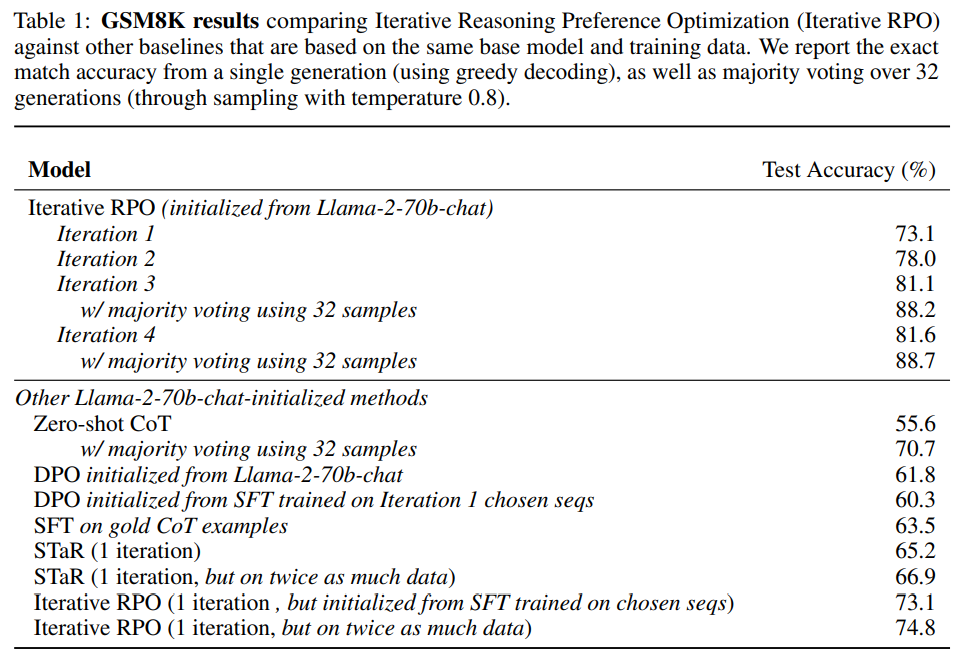
  • 학습을 하지 않았을 때, DPO를 돌렸을 때 성능이 55 ~ 70 사이인데 반해서, Iterative RPO를 하면 88%까지 정확도가 상승한다.
  • SFT 방식을 하면, 정답 CoT 데이터로 학습하던, STaR을 하던 성능이 66%정도인데 반해서, Iterative RPO를 하면 1 iteration에 70%를 상회하는 결과를 낸다.
• NLL loss의 효과
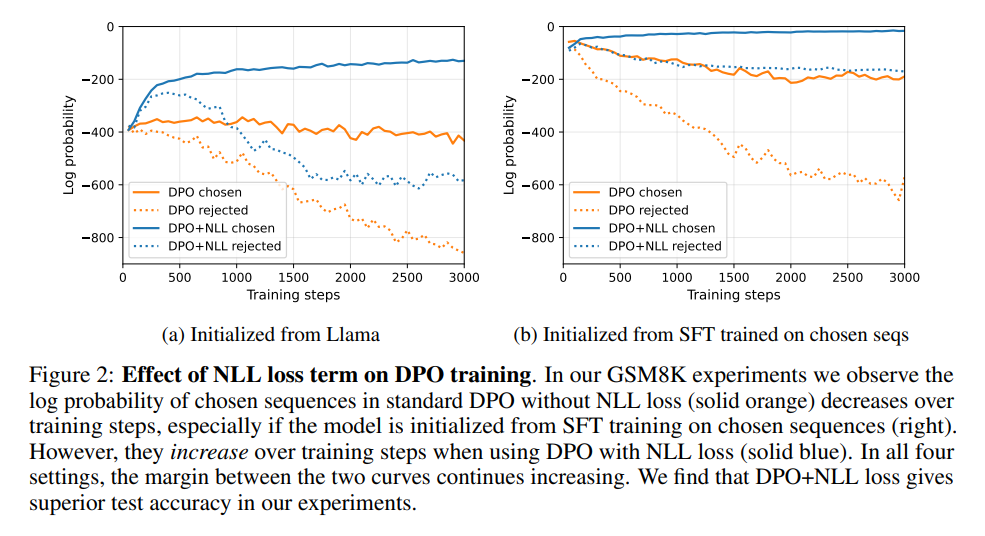
  • NLL을 사용한 모델이, DPO만 사용한 모델보다 실제 정답 sequence에서 확률이 더 높다.
• SFT와의 비교
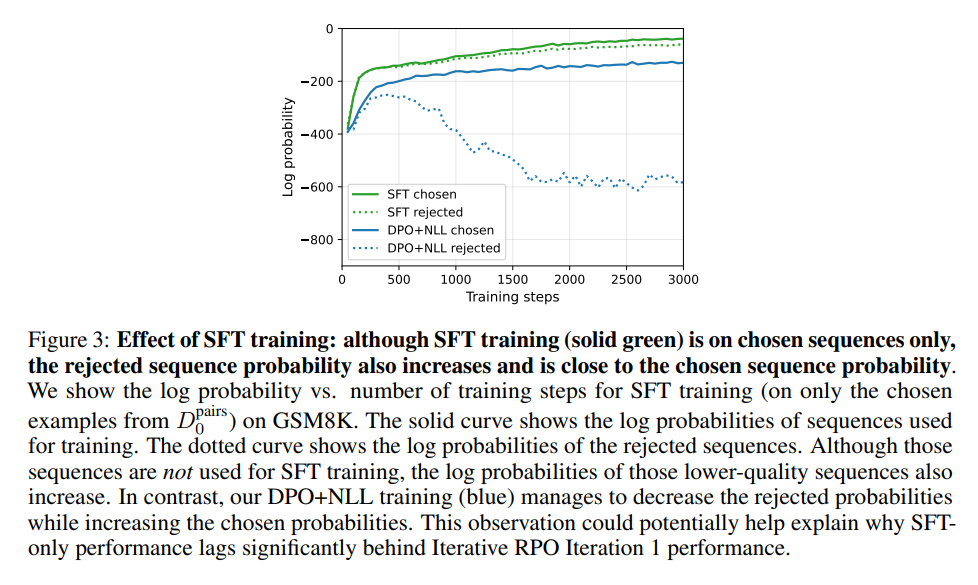
  • SFT가 log probability의 관점에서는 더 성능이 좋지만, rejected 샘플에 대해서도 확률이 올라간다 (그냥 많이 본 데이터에 대한 확률이 올라가는듯?). 따라서 실제 성능은 DPO + NLL 쪽이 더 좋은 것으로 보임
• ARC-challenge + MATH

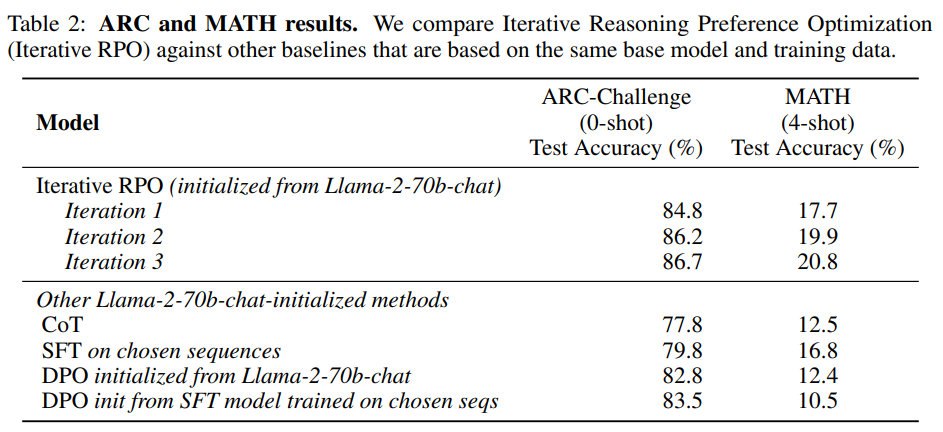
결론

• human feedback (preference)를 따로 수집하지 않고도, reasoning에서는 더 좋은 성능을 보인다.