DoRA, Weight-Decomposed Low-Rank Adaptation

논문 링크

• 논문 링크

배경

• LoRA를 위시로 한 PEFT 방법론이 널리 사용되고 있는데, full fine-tuning 방법과 비교했을 때 여전히 성능의 갭이 있다.
• 이 논문에서 그 갭의 원인을 파악하고, 이를 수정하는 DoRA라는 방법론을 제시한다.

성능 차이의 원인 파악

• 기존의 W를 magnitude와 direction으로 나누면, 아래와 같다.

  \[W=m\frac{V}{\lVert{V}\rVert_{c}} = \lVert{W}\rVert_C\frac{W}{\lVert{W}\rVert_c}\]
  • m은 magnitude, V는 direction. 분모는 vector-wise norm

• 추가 학습을 했을 때, 기존 W와의 magnitude와 direction 차이를 각각 나타내면 아래와 같다.

  \[\Delta{M}_{FT}^t = \frac{\Sigma_{n=1}^k |m_{FT}^{n,t} - m_0^n|}{k}\] \[\Delta{D}_{FT}^t = \frac{\Sigma_{n=1}^k (1 - \cos{(V_{FT}^{n,t}, W_0^n)})}{k}\]
  • 각각의 delta는 기존 weight와의 차이를 나타내고, cos은 cosine similarity 함수이다.
  • t는 training step, n은 n번째 컬럼을 나타낸다.
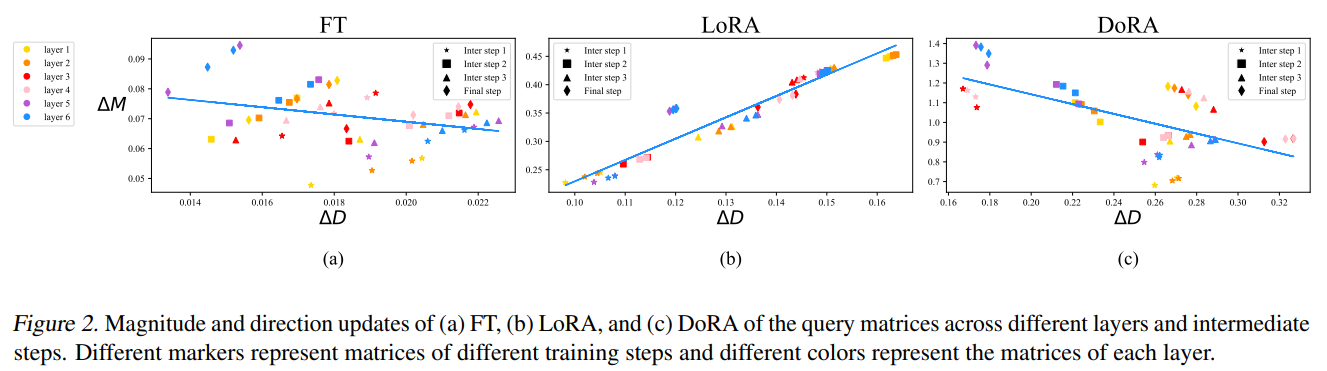
• 이렇게 정의하고 fine tune과 LoRA에 대해서 magnitude와 direction의 변화를 비교해보면, fine tuning은 거의 상관관계가 없거나 약간 음의 상관관계인 반면, LoRA는 강하게 양의 상관관계를 가지고 있다.
• 즉, LoRA는 magnitude와 direction을 동시에 증가시키거나 감소시키는 편인 반면, fine-tuning은 그렇지 않다. 따라서, LoRA는 미묘한 변화를 주기에 적절한 framework는 아니다.
• LoRA는 이걸 한 번에 학습하기 때문이라고 생각하고, 둘을 나눠서 학습하는 DoRA 방식을 고안함.

DoRA

• Weight matrix를 magnitude와 direction으로 쪼개고, 이를 각각 학습시킨다. magnitude 자체를 trainable parameter로 두고, direction에서 LoRA를 적용한다

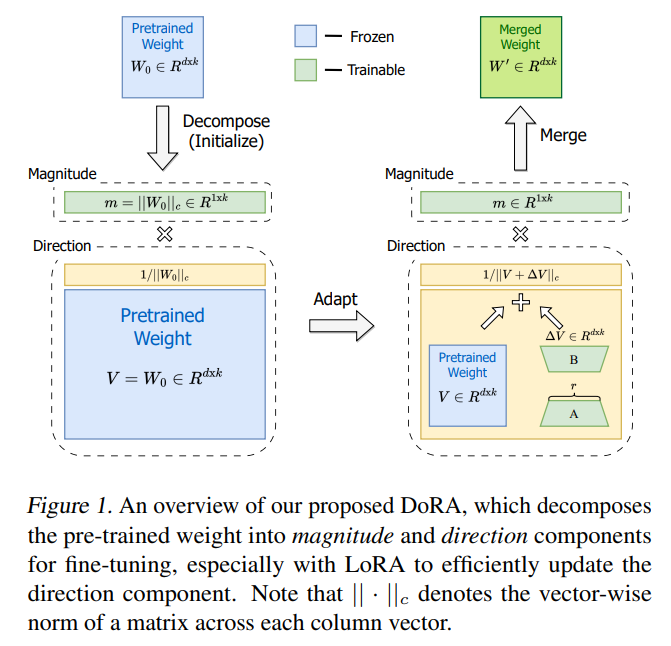
• 기존의 LoRA 방법은 새롭게 학습되는 W’을 아래와 같이 정의한다.

  \[W'=W_0 + \Delta{W} = W_0 + BA\]
  • A, B는 기존의 dimension보다 훨씬 작은 rank를 가진 매트릭스로, A는 Kaiming distribution을 따르게 초기화를 하고 B는 0으로 초기화한다.

• 같은 수식을 DoRA에 맞도록 쓰면,

  \[W'=m\frac{V+\Delta{V}}{\lVert{V+\Delta{V}}\rVert_c} = m\frac{W_0+BA}{\lVert{W_0+BA}\rVert_c}\]
  • m과 delta V가 learnable parameter. A,B는 LoRA와 같은 방식으로 초기화한다.
  • 이렇게 학습하면, 위의 그래프처럼 FT를 따라가고 (magnitude와 direction이 반비례함), LoRA와는 다른 패턴을 보인다.
• 작은 directional update와 큰 directional update를 가정했을 때, DoRA의 방법에 맞춰서 gradient를 계산해보면 큰 directional update가 더 작은 magnitude update를 하게 됨.

• 위의 수식대로 W’을 계산하면, 아래 수식이 가변적이기 때문에 메모리를 많이 차지하게 된다.

  \[\lVert{V+\Delta{V}}\rVert_c\]
• 그래서 이걸 그냥 C라고 하는 어떤 constant로 고정하면, gradient 수식이 변경되는데, 이를 통해 memory를 아낄 수 있다.

  • 이전

    \[\nabla_{V'}L = \frac{m}{\lVert{V'}\rVert_c}(I-\frac{V'V'^T}{\lVert{V'}\rVert_c^2})\nabla_{W'}L\]

  • 이후

    \[\nabla{V'}L = \frac{m}{C}\nabla_{W'}L\]

실험

• commensense reasoning
  • 8개의 task를 선정했고, LLaMA 7B, 13B에 대해서 Prompt learning, Series adapter, Parallel adapter, LoRA 와 비교했다.
  • LoRA 대비 parameter 숫자가 약간 큰 이유는 magnitude 때문이다. rank를 더 줄여도 LoRA보다 잘한다.
• multimodal
  • 거의 모든 task에 대해서 LoRA보다 잘한다.
• LoRA 계열의 다른 방법론에 적용해도 잘 한다.
  • VeRA는 unique pair를 모든 layer에 적용하는 방식(?) 인데 아무튼 parameter 수를 획기적으로 줄인다. 여기에 DoRA를 적용해도 성능이 꽤 향상됨.

• 학습 데이터의 양에도 robust 하다
  

• rank 등 hyperparameter에도 robust함

결론

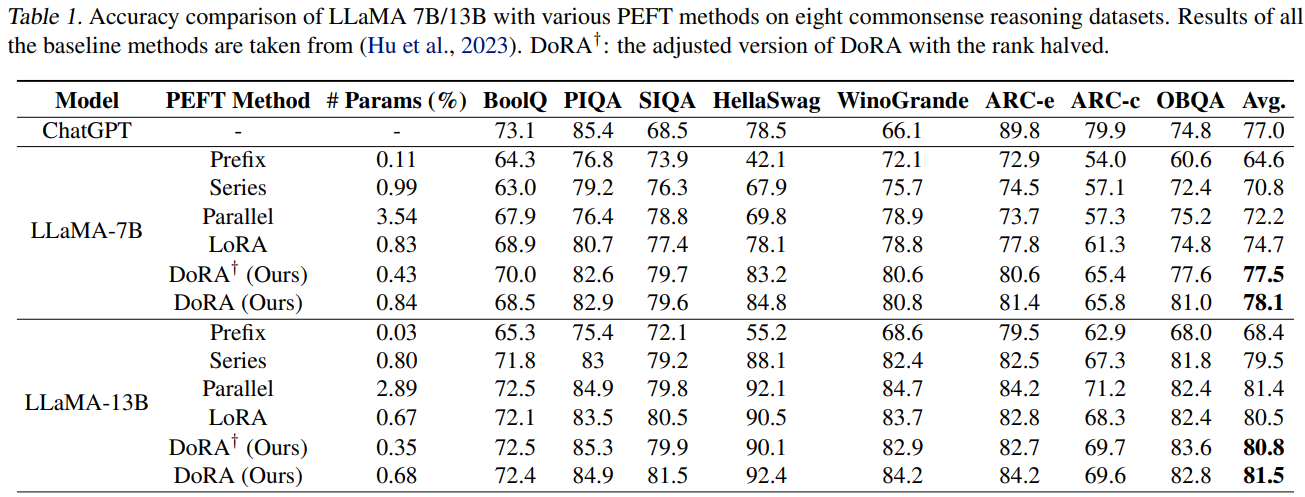
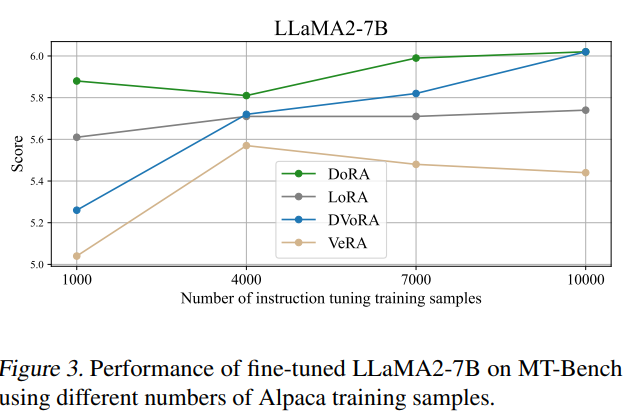
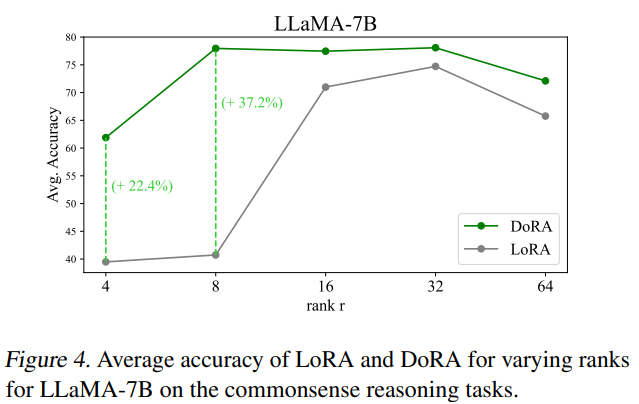
• LoRA에 비해서 trainable parameter가 아주 약간 상승하는 것을 제외하면 cost가 거의 들지 않는데, 성능은 유의미한 향상을 보인다.
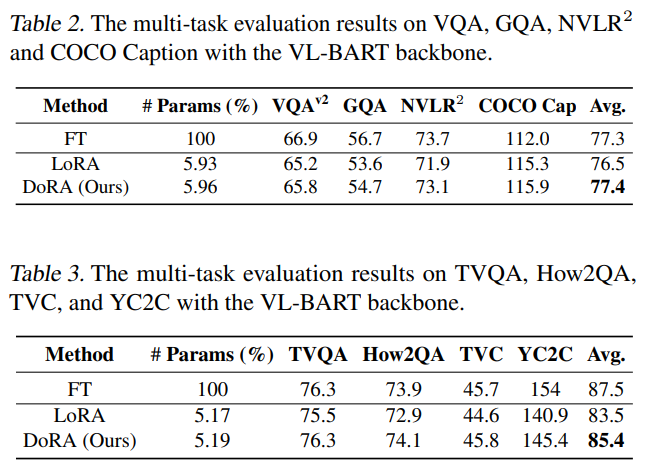
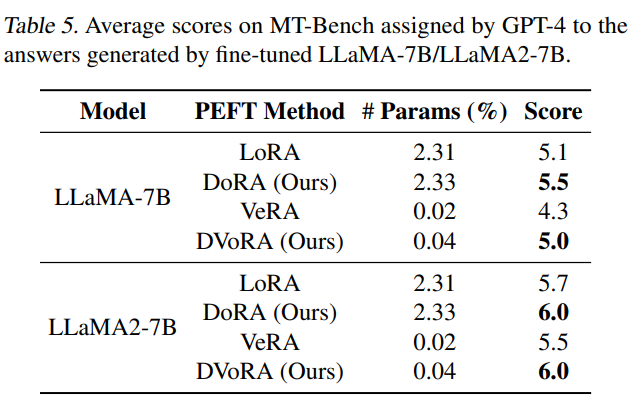
• 언어, 이미지, 비디오 등에서는 다 잘 되는 것으로 보임